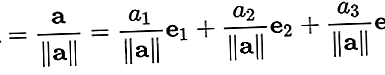Вектор в математиці та фізиці можна визначити як геометричні об'єкти, що мають величину і напрямок. Вектор зображений стрілкою, де в основі стрілки показана точка лову (початкова точка) вектора, довжина стрілки вказує на розмір або значення вектора (чим довша стрілка, тим більше значення або значення вектора, і навпаки), тоді як стрілка вказує напрямок вектора.
У письмовій формі, якщо вектор починається в точці A і закінчується в точці B, то його можна записати маленькою літерою, над якою є рядок / стрілка, як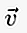 
або 
або 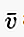також:
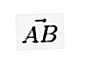
Типи векторів
Вектор в математиці поділяється на 4 типи, серед яких:
Позиція вектор
Вектор, початкова точка якого дорівнює 0 (0,0), а його закінчення - A (a1, a2).
Нульовий вектор
"Вектор нульовий" (нульовий вектор абонульовий вектор) - вектор, довжина якого дорівнює "нулю". Запис у цій векторній координаті дорівнює (0,0,0) і зазвичай отримує символ 
, або0. Цей вектор відрізняється від інших векторів тим, що його неможливо нормалізувати (тобто жоден одиничний вектор не кратний нульовому вектору). Кількість векторів дорівнює нулю з будь-яким векторомa єa (це,0+a=a).
Нульовий вектор не має чіткого напряму вектора.
Одиниця вектор
являє собою вектор довжиною "одиниця". Зазвичай одиничний вектор використовується лише для позначення напрямку. Вектор будь-якої довжини можна поділити на довжину, щоб отримати одиничний вектор. Це відомо як "нормалізуючий" вектор. Одиничний вектор часто позначається "кришкою" над малою літерою "а", як уâ.
Для нормалізації вектораa = [a1, a2, a3], розділіть вектор на довжину ||a||. Так:
Базовий вектор
Одиничний вектор, який перпендикулярний один до одного. У двовимірному просторовому векторі (Р.2) має два базові вектори, а саме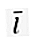 
= (1, 0) і 
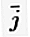= (0, 1).
Подібність двох векторів
Кажуть, що два вектори однакові, якщо вони мають однакову довжину та напрямок
Вирівнювання двох векторів
Два вектори називаються паралельними (паралельними), якщо пряма, що представляє два вектори, паралельна.
Векторні операції
Скалярне множення
Вектор можна помножити на скаляр, що також призводить до отримання вектора, результуючим вектором є:
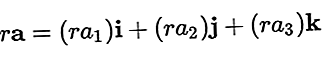
Складання і віднімання вектора
Як приклад вектора a=a1i + a2j + a3k іb=b1i + b2j + b3k
Результат плюс b: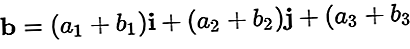 
скорочення вектора також застосовується, замінюючи знак + на знак -
